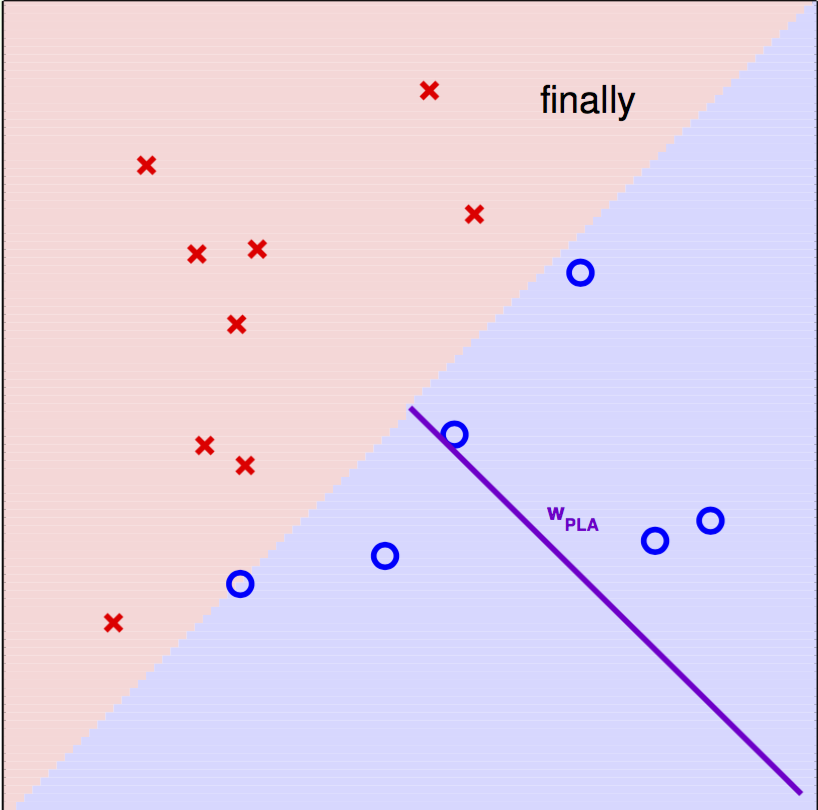
总结感知机及其对偶形式
问题背景
实际应用中常出现二元分类问题,如引用台湾大学机器学习基石课程[1]的信用卡案例:如有用户申请信用卡,其个人信息如下:
| 特征 | 数据 |
|---|---|
| 年龄 | 23 |
| 性别 | 女 |
| 年收入 | 1,000,000 |
| 居住年限 | 1 |
| 工作年限 | 0.5 |
| 负债 | 200,000 |
银行具有原来的信用卡申请记录(包括申请用户信息及审批结果),如何根据原来的记录判断当前申请是否能够批准就是一个典型的二分问题。输入数据为个人信息,训练数据为历史申请及审批记录,输出数据为是否同意申请。
假设银行根据申请用户的各项信息(特征)为用户打分,并且设定一个阈值,在用户得分超过该阈值则同意信用卡申请,否则拒绝申请。
故假设用户具m个特征为
得分阈值为$d$。每个特征对于最终的用户得分有不同的重要程度,所以为每一个特征增加入不同的权值$w=({w_1,w_2,\cdots,w_m})$,用户最终得分为
最后只需要比较 $\sum_{i=1}^{m}w_ix_i$与阈值$d$的大小就可以得出结果。
观察上文公式,如何确定每一个信息的权值$w$及同意申请的阈值$d$就是解决问题的关键,由于具有历史数据,使用历史数据确定参数的想法就水到渠成。
问题抽象
根据上文背景问题的提出,可进行抽象,银行n笔已知的数据可以抽象为训练数据集
其中$x\in\chi ,\chi\subseteq R^m$,$y\in\mathcal{Y}=\{+1,-1\}$。
设上文求和公式及阈值之差为函数
为简化公式取$b=-d$,则公式变化为:
改写为向量形式为:
当$h(x)>0$时,发放信用卡,否则拒绝发放信用卡
使用取符号的函数$sign$,得到函数
此函数为感知机算法需要学习得到的最终函数。
感知机介绍
感知机1957年由Rosenblatt提出,是支持向量机及神经网络基础算法。
感知机主要通过训练数据集学习函数:
中的模型参数$w$及$b$,其中$x\in\chi ,\chi\subseteq R^m,w\in R^m,b\in R$。感知机算法要求训练集是线性可分,当训练集线性可分时可以证明感知机算法可以通过有限次的搜索找到将训练集完全区分的超平面,否则感知机算法将不会收敛[2]。
未完待续
参考文献
[1] 林轩田.机器学习基石[R].台湾:台湾大学.
[2] 李航.统计学习方法[M].北京:清华大学出版社,2012:26-33.